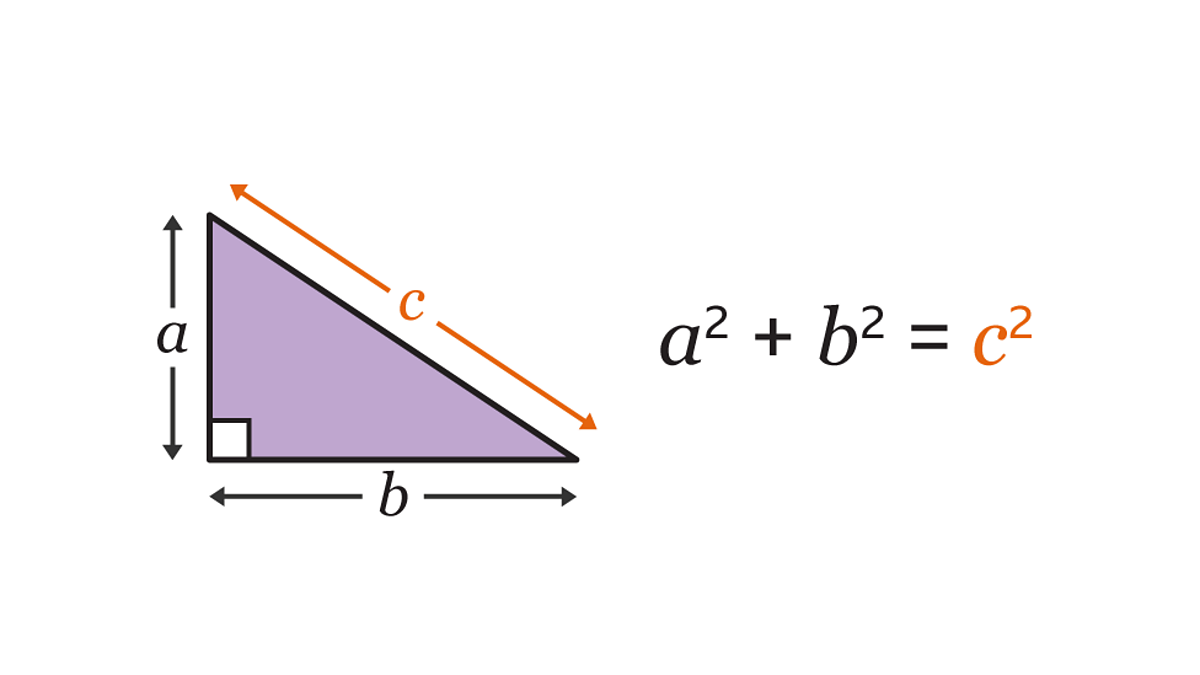
The Pythagorean Theorem is one of the most fundamental ideas in geometry, especially when it comes to right triangles. It gives us a reliable way to find the length of one side of a right triangle when the other two are known.
The theorem is named after the ancient Greek mathematician Pythagoras, and it states:
$$a^2 + b^2 = c^2$$
Where:
aandbare the two legs of a right triangle (the sides that form the right angle)cis the hypotenuse, or the side opposite the right angle
Why is this important in Math?
This formula is extremely useful in many real-world and academic applications. It lets you calculate distances, heights, and diagonal lengths without needing to physically measure them.
How does it work?
Imagine you have a triangle where one side is 3 units long, another is 4 units long, and you want to know the length of the hypotenuse.
$$
3^2 + 4^2 = c^2 \\
9 + 16 = c^2 \\
25 = c^2 \\
c = 5
$$
So the hypotenuse is 5 units long.
Real-life Applications
House Construction
Kapag gumagawa ng hagdanan, kailangang tama ang sukat ng steps para hindi ito maging delikado. Halimbawa, kung ang step ay 4 feet ang taas at 6 feet ang haba, pwede mong gamitin ang Pythagorean Theorem para malaman ang haba ng kahoy na gagamitin bilang diagonal step:
$$4^2 + 6^2 = c^2 \Rightarrow 16 + 36 = 52 \Rightarrow c = \sqrt{52} \approx 7.2 \text{ feet}$$
Shortcut Planning
Kung gusto mong gumawa ng shortcut papunta sa isang kanto mula sa kabilang kalsada, imbes na sundan ang “L” shape ng daan, sukatin mo na lang ang diagonal. Kunwari 100 meters ang diretsong daan at 75 meters ang patagilid, ang shortcut ay:
$$100^2 + 75^2 = c^2 \Rightarrow 10000 + 5625 = 15625 \Rightarrow c = \sqrt{15625} = 125 \text{ meters}$$
Tip to Remember
Always make sure you’re dealing with a right triangle before applying the theorem. If the angle isn’t 90 degrees, it won’t work.
Conclusion
The Pythagorean Theorem isn’t just a classroom formula—it’s a powerful tool that helps us measure and build in the real world. From staircases to roads to architecture, this simple equation has stood the test of time.